Case study Questions on the Class 10 Mathematics Chapter 10 are very important to solve for your exam. Class 10 Maths Chapter 10 Case Study Questions have been prepared for the latest exam pattern. You can check your knowledge by solving case study-based questions for Class 10 Maths Chapter 10 Circles
In CBSE Class 10 Maths Paper, Students will have to answer some questions based on Assertion and Reason. There will be a few questions based on case studies and passage-based as well. In that, a paragraph will be given, and then the MCQ questions based on it will be asked.
Circles Case Study Questions With answers
Here, we have provided case-based/passage-based questions for Class 10 Maths Chapter 10 Circles
Case Study/Passage Based Questions
Smita always finds it confusing with the concepts of tangent and secant of a circle. But this time she has determined herself to get concepts easier. So, she started listing down the differences between tangent and secant of a circle along with their relation. Here, some points in question form are listed by Smita in her notes.
A line that intersects a circle exactly at two points is called
(a) Secant (b) Tangent
(c) Chord (d) Both (a) and (b)
Answer: (a) Secant
The number of tangents that can be drawn on a circle is
(a) 1 (b) 0 (c) 2 (d) Infinite
Answer: (d) Infinite
The number of tangents that can be drawn to a circle from a point, not on it, is
(a) 1 (b) 2 (c) 0 (d) Infinite
Answer: (b) 2
Number of secants that can be drawn to a circle from a point on it is
(a) infinite (b) 1 (c) 2 (d) 0
Answer: (a) infinite
A line that touches a circle at only one point is called
(a) Secant (b) Chord
(c) Tangent (d) Diameter
Answer: (c) Tangent
Case Study/Passage Based Questions
If a tangent is drawn to a circle from an external point, then the radius at the point of contact is perpendicular to the tangent.
Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
(a) 8 cm (b) 4 cm (c) 10 cm (d) 6 cm
Answer: (a) 8 cm
In the given figure, O is the centre of two concentric circles of radii 5 cm and 3 cm. From an external point P tangent, PA and PB are drawn to these circles. If PA = 12 cm, then PB =
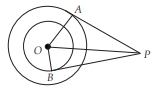
(a) 2√10 cm (b) 2√5 cm
(c) 4√10 cm (d) 4√5 cm
Answer: (c) 4√10 cm
The diameter of the two concentric circles is 10 cm and 6 cm. AB is the diameter of the bigger circle and BD is the tangent to the smaller circle touching it at D and intersecting the larger circle at P on producing. Find the length of BP.
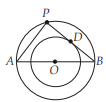
Answer: (d) 8 cm
Two concentric circles are such that the difference between their radii is 4 cm and the length of the chord of the larger circle which touches the smaller circle is 24 cm. Then the radius of the smaller circle is
(a) 16 cm (b) 20 cm
(c) 18 cm (d) None of these
Answer: (a) 16 cm
Hope the information shed above regarding Case Study and Passage Based Questions for Class 10 Maths Chapter 10 Circles with Answers Pdf free download has been useful to an extent. If you have any other queries of CBSE Class 10 Maths Circles Case Study and Passage Based Questions with Answers, feel free to comment below so that we can revert back to us at the earliest possible
By Team Study Rate
