
Introduction
Science is the meeting point of pure mathematics and the real world. Every measurement and computation must be documented, and using standard form and significant digit notation helps us to document what is relevant while avoiding the need to write a Lot of irrelevant numbers.
The concept of standard form was invented by Archimedes, while Rene Descartes developed the technique that modern mathematicians use to express numbers.
According to Arithmetic, the advantage of standard form is that it allows scientists to manipulate extremely large and small numbers without having to deal with place value extremes.
Counting lots of 0s while typing or reading is much more error prone than formatting an exponent incorrectly, and it is much more difficult to detect when an error occurs.
Computer programs and calculators can be configured to display results in scientific notation, which significantly reduces the chances of numerical expression mistakes, giving standard form a significant advantage.
Definition
“Standard form is a method of representing the absolute value of very large or very small integers as one decimal number larger than 1 and less than 10, multiplied by the corresponding integer power of 10”.
A number N is expressed in scientific notation if
|N| = n x 10^k
Where 1 < n < 10 and k is an integer.
Method to convert a number in standard form
- Shift the decimal place in your number unless there is just one non-zero digit to the left of the decimal point. The generated decimal number is a.
- Count the times you shifted the decimal point. This is the number k.
- If you shift the decimal point to the left, k becomes positive.
- If you shift the decimal point to the right, k becomes negative.
- If you didn’t have to change the decimal point, k = 0.
- Write your number in scientific notation as an n x 10^k and interpret it as “a times 10 to the power of k.
- Only remove trailing 0s if they are to the left of the decimal point.
Types
Standard form can be represented into different types such as
- Engineering notation
- E-notation
Engineering notation
“Engineering notation is similar to scientific notation, with the exception that the exponent, n, must be a multiple of three, such as 0, 3, 6, 9, 12, -3, -6, and so on”.
The numbers are aligned with SI prefixes and can be read as such as a result of this. For example, the kilo prefix would be used on 103, the mega prefix on 106, and the giga prefix on 109.
To convert scientific notation to engineering notation, the decimal position of the integer might be moved. For example
52548872 can be converted as 52.54 × 106.
E-notation
“The “10” in scientific notation is substituted with just “E” in E-notation”.
It’s utilised when displaying the exponent is difficult.
It’s spelled out as
nEk
Where n is the basis, k stands for “x 10,” and k comes after the E. An example of comparison between scientific notation and E-notation is shown below.
5.3 x 106 can be written as 5.3E6.
How to calculate the problems of standard form?
Example 1:
The Sun and Mars are separated by 141,700,000 miles (228,000,000 km). Write their distance in standard form.
Solution: Manual method
Step 1: Shift the decimal point to the first non-zero digit
1.41700000 miles and 2.28000000 km
Step2: Now count the number of digits after decimal point. Write the counted number of digits in power of 10.
1.41 × 108 miles and 2.28 × 108 km
Hence the standard form is calculated.
In terms of engineering notation and E-notation we can write above figures as
1.41 × 106 miles and 2.28 × 106 km
1.41E8 miles and 2.28E8km
Hence the engineering notation and E-notation is also calculated.
The following problem can also be solved using a standard notation calculator. It enables us to solve issues fast and effectively by utilising a scientific method. It breaks down the problem into small bits, allowing pupils to spend more time understanding it. The problems can be handled by just a single click.
Solution: By using calculator
Step 1: Place the given data values into the calculator and press the convert button.

Congratulations your standard form has been calculated.
Example 2:
The diameter of an atom is 0.0000000001m. Convert it in standard form
Solution: Manual method
Step 1: Shift the decimal point to the first non-zero digit
00000000001.0 m
Step2: Now count the number of digits after decimal point. Write the counted number of digits in power of 10.
1.0 × 10-10 m
Hence the standard form is calculated.
In terms E-notation we can write above figures as
1.0E-10 m
Solution: By using calculator
Step 1: Place the given data values into the standard form calculator and press the convert button.

Hence the standard form is calculated.
Example 3:
The speed of light is 300000000ms-1. Calculate its standard form.
Solution: Manual method
Step 1: Shift the decimal point to the first non-zero digit
3.00000000ms-1
Step2: Now count the number of digits after decimal point. Write the counted number of digits in power of 10.
3.0 × 108 ms-1
Hence the standard form is calculated.
In terms E-notation we can write above figures as
3E8
Solution: By using calculator
Step 1: Place the given data values into the calculator and press the convert button.
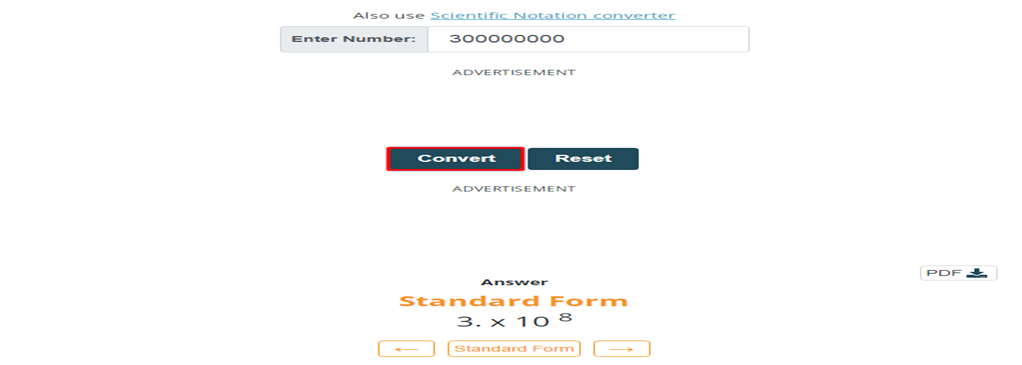
Hence the standard form is calculated.
Summary:
Extremely small and extremely high numbers are frequently encountered in physics. These figures can be expressed more efficiently whenever they are written in scientific notation.
It is the most straightforward method of dealing with numbers that you will meet in a scientific setting.
It is just a distinction between precision and accuracy. Decimals offer precision but not accuracy, because erroneous precision has no value.
Rather, only a few digits are required for accuracy; the remainder is determined by the magnitude of the scale.
It is used by physicists to write exceedingly large or small amounts. Numbers that would normally require ridiculous amounts of preceding or trailing zeroes.
