Download Class 9 Maths Case Study Questions to prepare for the upcoming CBSE Class 9 Exams 2023-24. These Case Study and Passage Based questions are published by the experts of CBSE Experts for the students of CBSE Class 9 so that they can score 100% in Exams.
Case study questions play a pivotal role in enhancing students’ problem-solving skills. By presenting real-life scenarios, these questions encourage students to think beyond textbook formulas and apply mathematical concepts to practical situations. This approach not only strengthens their understanding of mathematical concepts but also develops their analytical thinking abilities.
CBSE Class 9th MATHS: Chapterwise Case Study Questions
Inboard exams, students will find the questions based on assertion and reasoning. Also, there will be a few questions based on case studies. In that, a paragraph will be given, and then the MCQ questions based on it will be asked. For Class 9 Maths Case Study Questions, there would be 5 case-based sub-part questions, wherein a student has to attempt 4 sub-part questions.

Chapterwise Case Study Questions of Class 9 Maths
- Case Study Questions for Chapter 1 Number System
- Case Study Questions for Chapter 2 Polynomials
- Case Study Questions for Chapter 3 Coordinate Geometry
- Case Study Questions for Chapter 4 Linear Equations in Two Variables
- Case Study Questions for Chapter 5 Introduction to Euclid’s Geometry
- Case Study Questions for Chapter 6 Lines and Angles
- Case Study Questions for Chapter 7 Triangles
- Case Study Questions for Chapter 8 Quadrilaterals
- Case Study Questions for Chapter 9 Areas of Parallelograms and Triangles
- Case Study Questions for Chapter 10 Circles
- Case Study Questions for Chapter 11 Constructions
- Case Study Questions for Chapter 12 Heron’s Formula
- Case Study Questions for Chapter 13 Surface Area and Volumes
- Case Study Questions for Chapter 14 Statistics
- Case Study Questions for Chapter 15 Probability
Checkout: Class 9 Science Case Study Questions
And for mathematical calculations, tap Math Calculators which are freely proposed to make use of by calculator-online.net
The above Class 9 Maths Case Study Questions will help you to boost your scores as Case Study questions have been coming in your examinations. These CBSE Class 9 Maths Case Study Questions have been developed by experienced teachers of cbseexpert.com for the benefit of Class 10 students.
Class 9 Maths Syllabus 2023-24
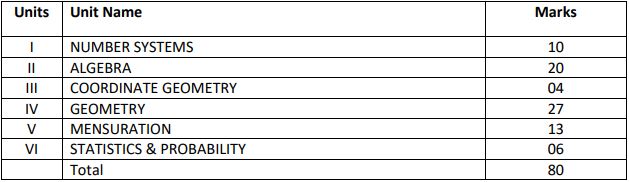
UNIT I: NUMBER SYSTEMS
1. REAL NUMBERS (18 Periods)
1. Review of representation of natural numbers, integers, and rational numbers on the number line. Rational numbers as recurring/ terminating decimals. Operations on real numbers.
2. Examples of non-recurring/non-terminating decimals. Existence of non-rational numbers (irrational numbers) such as √2, √3 and their representation on the number line. Explaining that every real number is represented by a unique point on the number line and conversely, viz. every point on the number line represents a unique real number.
3. Definition of nth root of a real number.
4. Rationalization (with precise meaning) of real numbers of the type

(and their combinations) where x and y are natural number and a and b are integers.
5. Recall of laws of exponents with integral powers. Rational exponents with positive real bases (to be done by particular cases, allowing learner to arrive at the general laws.)
UNIT II: ALGEBRA
1. POLYNOMIALS (26 Periods)
Definition of a polynomial in one variable, with examples and counter examples. Coefficients of a polynomial, terms of a polynomial and zero polynomial. Degree of a polynomial. Constant, linear, quadratic and cubic polynomials. Monomials, binomials, trinomials. Factors and multiples. Zeros of a polynomial. Motivate and State the Remainder Theorem with examples. Statement and proof of the Factor Theorem. Factorization of ax2 + bx + c, a ≠ 0 where a, b and c are real numbers, and of cubic polynomials using the Factor Theorem. Recall of algebraic expressions and identities. Verification of identities:
RELATED STORIES
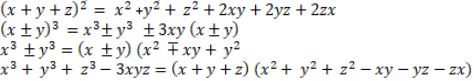
and their use in factorization of polynomials.
2. LINEAR EQUATIONS IN TWO VARIABLES (16 Periods)
Recall of linear equations in one variable. Introduction to the equation in two variables. Focus on linear equations of the type ax + by + c=0.Explain that a linear equation in two variables has infinitely many solutions and justify their being written as ordered pairs of real numbers, plotting them and showing that they lie on a line.
UNIT III: COORDINATE GEOMETRY COORDINATE GEOMETRY (7 Periods)
The Cartesian plane, coordinates of a point, names and terms associated with the coordinate plane, notations.
UNIT IV: GEOMETRY
1. INTRODUCTION TO EUCLID’S GEOMETRY (7 Periods)
History – Geometry in India and Euclid’s geometry. Euclid’s method of formalizing observed phenomenon into rigorous Mathematics with definitions, common/obvious notions, axioms/postulates and theorems. The five postulates of Euclid. Showing the relationship between axiom and theorem, for example: (Axiom)
1. Given two distinct points, there exists one and only one line through them. (Theorem)
2. (Prove) Two distinct lines cannot have more than one point in common.
2. LINES AND ANGLES (15 Periods)
1. (Motivate) If a ray stands on a line, then the sum of the two adjacent angles so formed is 180O and the converse.
2. (Prove) If two lines intersect, vertically opposite angles are equal.
3. (Motivate) Lines which are parallel to a given line are parallel.
3. TRIANGLES (22 Periods)
1. (Motivate) Two triangles are congruent if any two sides and the included angle of one triangle is equal to any two sides and the included angle of the other triangle (SAS Congruence).
2. (Prove) Two triangles are congruent if any two angles and the included side of one triangle is equal to any two angles and the included side of the other triangle (ASA Congruence).
3. (Motivate) Two triangles are congruent if the three sides of one triangle are equal to three sides of the other triangle (SSS Congruence).
4. (Motivate) Two right triangles are congruent if the hypotenuse and a side of one triangle are equal (respectively) to the hypotenuse and a side of the other triangle. (RHS Congruence)
5. (Prove) The angles opposite to equal sides of a triangle are equal.
6. (Motivate) The sides opposite to equal angles of a triangle are equal.
4. QUADRILATERALS (13 Periods)
1. (Prove) The diagonal divides a parallelogram into two congruent triangles.
2. (Motivate) In a parallelogram opposite sides are equal, and conversely.
3. (Motivate) In a parallelogram opposite angles are equal, and conversely.
4. (Motivate) A quadrilateral is a parallelogram if a pair of its opposite sides is parallel and equal.
5. (Motivate) In a parallelogram, the diagonals bisect each other and conversely.
6. (Motivate) In a triangle, the line segment joining the mid points of any two sides is parallel to the third side and in half of it and (motivate) its converse.
5. CIRCLES (17 Periods)
1. (Prove) Equal chords of a circle subtend equal angles at the center and (motivate) its converse.
2. (Motivate) The perpendicular from the center of a circle to a chord bisects the chord and conversely, the line drawn through the center of a circle to bisect a chord is perpendicular to the chord.
3. (Motivate) Equal chords of a circle (or of congruent circles) are equidistant from the center (or their respective centers) and conversely.
4. (Prove) The angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle.
5. (Motivate) Angles in the same segment of a circle are equal.
6. (Motivate) If a line segment joining two points subtends equal angle at two other points lying on the same side of the line containing the segment, the four points lie on a circle.
7. (Motivate) The sum of either of the pair of the opposite angles of a cyclic quadrilateral is 180° and its converse.
UNIT V: MENSURATION 1.
1. AREAS (5 Periods)
Area of a triangle using Heron’s formula (without proof)
2. SURFACE AREAS AND VOLUMES (17 Periods)
Surface areas and volumes of spheres (including hemispheres) and right circular cones.
UNIT VI: STATISTICS & PROBABILITY
STATISTICS (15 Periods)
Bar graphs, histograms (with varying base lengths), and frequency polygons.
To crack case study questions, Class 9 Mathematics students need to apply their mathematical knowledge to real-life situations. They should first read the question carefully and identify the key information. They should then identify the relevant mathematical concepts that can be applied to solve the question. Once they have done this, they can start solving the Class 9 Mathematics case study question.
Benefits of Practicing CBSE Class 9 Maths Case Study Questions
Regular practice of CBSE Class 9 Maths case study questions offers several benefits to students. Some of the key advantages include:
- Deeper Understanding: Case study questions foster a deeper understanding of mathematical concepts by connecting them to real-world scenarios. This improves retention and comprehension.
- Practical Application: Students learn to apply mathematical concepts to practical situations, preparing them for real-life problem-solving beyond the classroom.
- Critical Thinking: Case study questions require students to think critically, analyze data, and devise appropriate solutions. This nurtures their critical thinking abilities, which are valuable in various academic and professional domains.
- Exam Readiness: By practicing case study questions, students become familiar with the question format and gain confidence in their problem-solving abilities. This enhances their readiness for CBSE Class 9 Maths exams.
- Holistic Development: Solving case study questions cultivates not only mathematical skills but also essential life skills like analytical thinking, decision-making, and effective communication.
Tips to Solve CBSE Class 9 Maths Case Study Questions Effectively
Solving case study questions can be challenging, but with the right approach, you can excel. Here are some tips to enhance your problem-solving skills:
- Read the case study thoroughly and understand the problem statement before attempting to solve it.
- Identify the relevant data and extract the necessary information for your solution.
- Break down complex problems into smaller, manageable parts to simplify the solution process.
- Apply the appropriate mathematical concepts and formulas, ensuring a solid understanding of their principles.
- Clearly communicate your solution approach, including the steps followed, calculations made, and reasoning behind your choices.
- Practice regularly to familiarize yourself with different types of case study questions and enhance your problem-solving speed.Class 9 Maths Case Study Questions
Remember, solving case study questions is not just about finding the correct answer but also about demonstrating a logical and systematic approach. Now, let’s explore some resources that can aid your preparation for CBSE Class 9 Maths case study questions.
FAQ
Q1. Are case study questions included in the Class 9 Maths Case Study Questions syllabus?
Yes, case study questions are an integral part of the CBSE Class 9 Maths syllabus. They are designed to enhance problem-solving skills and encourage the application of mathematical concepts to real-life scenarios.
Q2. How can solving case study questions benefit students?
Solving case study questions enhances students’ problem-solving skills, analytical thinking, and decision-making abilities. It also bridges the gap between theoretical knowledge and practical application, making mathematics more relevant and engaging.
Q3. How do case study questions help in exam preparation?
Case study questions help in exam preparation by familiarizing students with the question format, improving analytical thinking skills, and developing a systematic approach to problem-solving. Regular practice of case study questions enhances exam readiness and boosts confidence in solving such questions.
